Elliptic Curve Torus

Materials and Methods: Knitted and sewn
Designer & Artist: Susan Schmoyer
Year: 2013--2014
Complex elliptic curves admit a both a description as an
equation of the form y2 = 4x3-ax-b and as a torus. On the equation
side, we can consider solutions in rational numbers x, y.
This piece shows the generators for all rational solutions
for the elliptic curve, y2 = 4x3 - (6750/49)x - (-13500/49), as points sewn onto
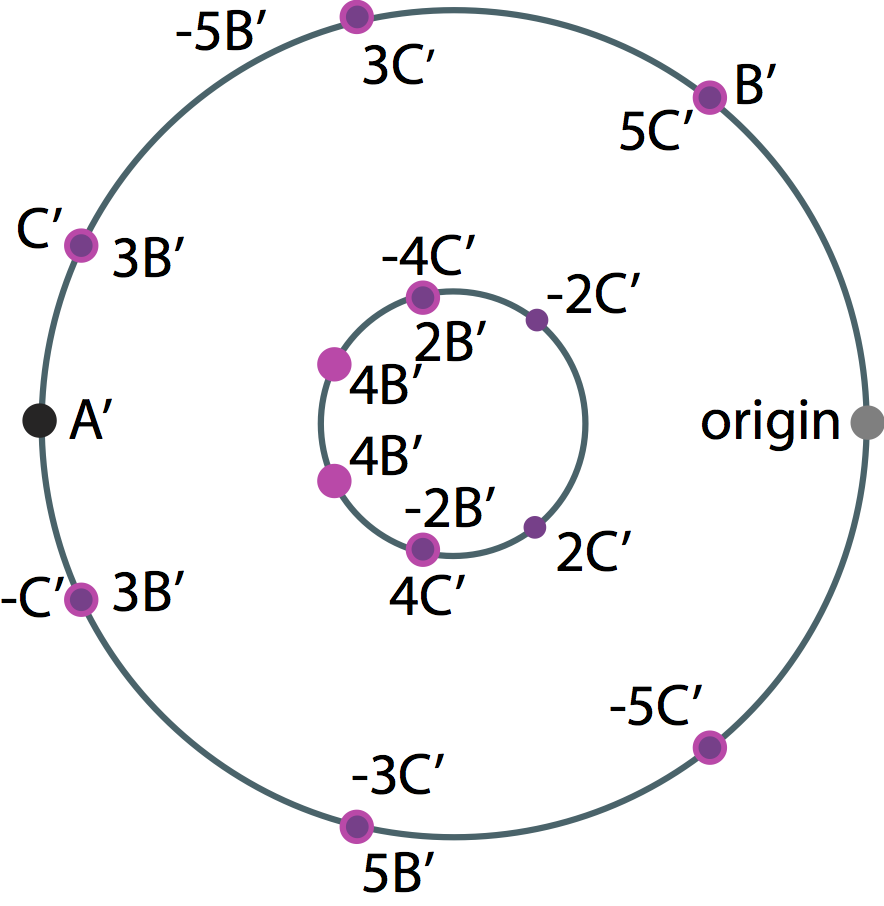
the corresponding torus. The set of all rational solutions is isomorphic to Z2 + Z + Z.
Let A
represent the generator of order 2; let B and C denote the generators of infinite order.
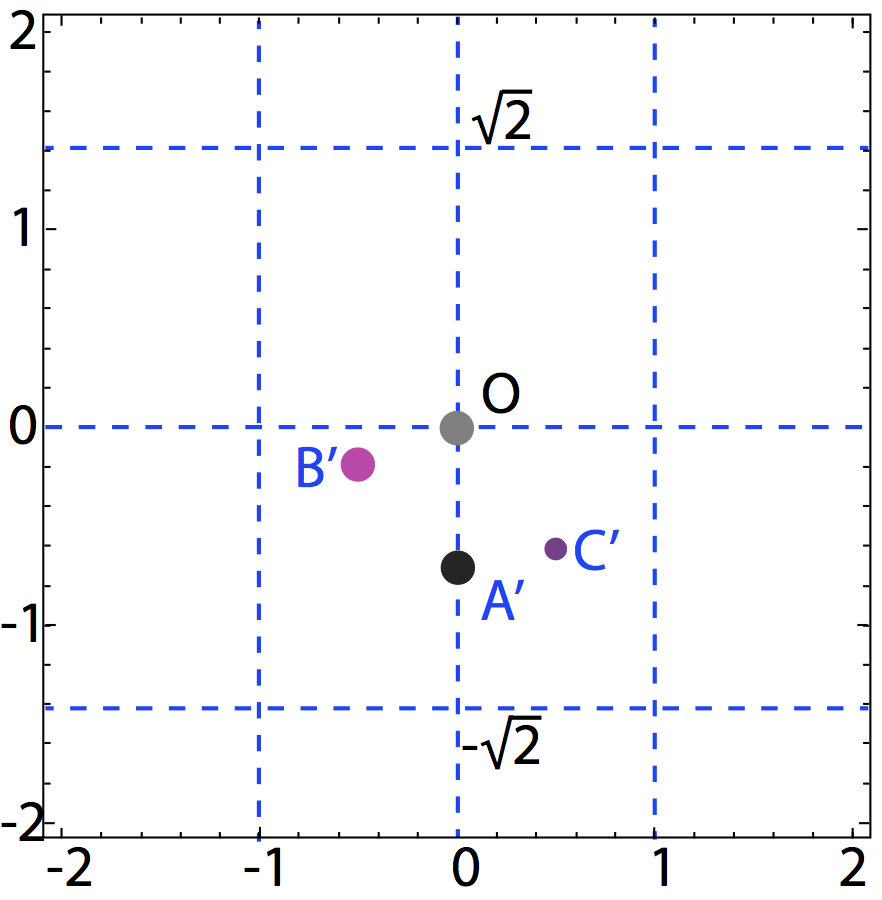
We invert the Weierstrass parametrization, wp(z),
to convert A, B, and C into points on the torus, called A', B', and C' (see below).
The point A' is sewn onto the torus as a dark grey point (see below-er).
The point B' and several of its integer multiples are sewn on as magenta points.
The point C' and several of its integer multiples are sewn on as purple points.
The origin is depicted as a light grey point.