Tilings of Sierpinski Relative Fractals

Designer and Artist: Larry Riddle
Materials and Methods: Cross Stitch on 22-count canvas
Years of Creation: 2021 and 2022

Designer and Artist: Larry Riddle
Materials and Methods: Cross Stitch on 22-count canvas
Years of Creation: 2021 and 2022
The two Sierpinski Relative fractal variations shown at right are constructed by recursively dividing a square into four equal squares, deleting one of these, fixing one, and rotating the other two by a non-zero multiple of \({\pi}/{2}\) radians counterclockwise. You can see in the images how the blue and green pieces are rotated relative to the fixed red piece. Tiles are formed by rotating copies of each relative by \({\pi}/{2}\) around a common center point, as shown in the images below.
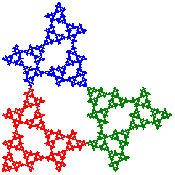
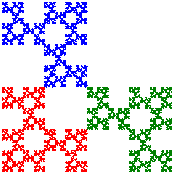
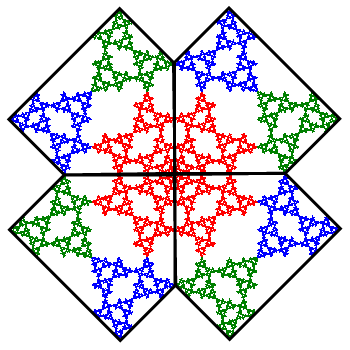
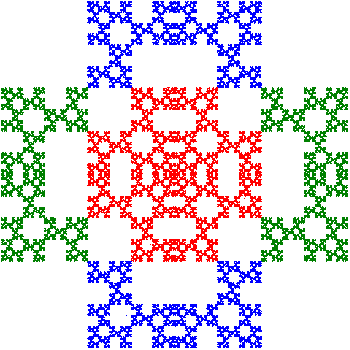
A cross stitch design can only approximately display each relative as the count size of the canvas and the desired frame size determine the maximum number of possible iterations. These pieces were stitched with seven iterations. The \(3^7=2187\) remaining squares in the construction are each stitched with one cross stitch. In one of the tilings, each of the smaller pieces actually consists of three different shades of that color to illustrate the self-similar nature of a fractal. If only the design is considered but not the colors, then each tiling also has reflective symmetry across horizontal, vertical, and diagonal lines through the center, thus representing the 8 transformations in the symmetry group of the square (also known as the dihedral group of order 8).
For more information about the mathematical properties of Sierpinski relatives and their tilings, visit my website on classic iterated function systems.